RStudio

En las entradas precedentes del blog  he usado, hasta ahora, R-Commander como interfaz que simplifica nuestra relación con R, especialmente al principio. Y sigo pensando que es un buen programa para principiantes, y continuaré explicando las opciones que ofrece.  Tengo además una deuda de gratitud con ese programa, porque mis primeros pasos con R habrían sido mucho más difíciles si no hubiera descubierto R-Commander (y el paquete R-UCA de la Universidad de Cádiz).

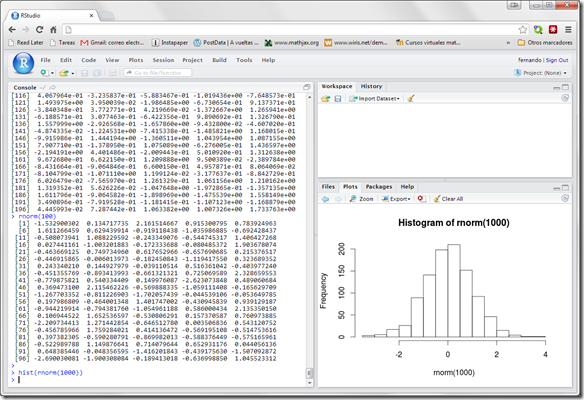
Sin embargo, en los últimos tiempos me he dejado convencer por otra interfaz gráfica de R, que se llama R-Studio (el enlace es la página principal del proyecto). Para presentarlo, aquí tenemos una captura de pantalla de RStudio, en una sesión de trabajo con el código de la entrada sobre ANOVA para diseños factoriales (con tres factores en este caso).

RStudio ofrece muchas herramientas para el usuario avezado de R, convirtiéndose en un entorno de trabajo muy productivo. Esa es la mayor diferencia con R-Commander, que tal vez está más orientado a proporcionar al usuario una experiencia  similar a la de los programas comerciales clásicos, donde los análisis están disponibles mediante un sistema de menús y cuadros de diálogo, como este:

En RStudio no encontraremos nada de eso. No hay un menú que nos diga cómo hacer un contraste de hipótesis, un intervalo de confianza. Para eso está R. En ese sentido, RStudio da por sentado que nosotros sabemos pedirle a R que haga esos análisis. Y por eso, para un principiante, puede resultar algo más intimidatorio.

Para el usuario con algo más de experiencia, como decíamos, la situación se invierte, y RStudio se muestra como una de las mejores opciones para el trabajo diario con R. Entre otras, quiero destacar estas características:

• la posibilidad de trabajar con varios ficheros de comandos R simultáneamente, agrupados por pestañas (en la ventana superior izquierda, en la anterior captura de pantalla).
• el editor de comandos es, en si mismo, una de las grandes virtudes de RStudio. Es realmente un editor pensado por y para programar en R. No echaremos en falta un editor externo, al que en general teníamos que recurrir con R-Commander.
• autocompletado de comandos. Si no recordamos la sintaxis exacta de un comando de R, basta con escribir las primeras letras, pulsar la tecla Tab, y RStudio nos ofrece información sobre ese comando. Pero también sobre las variables, ficheros y demás objetos que hayamos creado.
• gestión de los gráficos de R mucho más eficaz que, por ejemplo, en R-Commander.
• facilidad de gestión para, por ejemplo, instalar paquetes, consultar ayuda, etcétera.
• si se dispone de varias versiones de R instaladas en la máquina, es fácil seleccionar la que utilizará en cada sesión.

Pero además, RStudio ofrece la posibilidad de instalación en un servidor (bajo Linux), para posteriormente acceder al programa a través de una interfaz web, desde cualquier máquina, aunque no esté instalado R. Esa interfaz web es esencialmente idéntica a la que hemos mostrado más arriba, como puede verse en esta figura:

Esto hace posible (aunque desde luego, no muy cómodo) acceder a RStudio desde un teléfono móvil. Y desde luego es especialmente interesante para usuarios de tablets, (tanto Ipads como Android).

Para finalizar esta primera visita, en la página del proyecto RStudio se puede ver otro producto, Shiny, del que hablaremos en una futura entrada y que permite convertir los análisis que hacemos con R en páginas web interactivas, para que cualquier pueda experimentar con esos análisis, y modificar los parámetros utilizando deslizadores, cajas de diálogo, etc.  Una muestra, en este enlace.

Shiny  es una forma de avanzar en la idea de mostrar a los demás nuestro trabajo, cada vez de forma más trasparente. Una idea que está en la base del movimiento hacia lo que se ha llamado Investigación reproducible (Reproducible Research, página en la Wikipedia). En esencia, la idea es que los trabajos de investigación, a la hora de publicar sus resultados, debería acompañar la publicación tradicional con el conjunto completo de datos experimentales y los ficheros de código del software que se haya utilizado para el análisis de esos datos.

R tiene una herramienta muy poderosa para contribuir a esta idea, llamada SWeave. Y en esta entrada no puedo dejar de mencionar que RStudio (a diferencia de R-Commander) ofrece mucha ayuda para el trabajo con SWeave. Pero ese un tema que merece ser tratado con mucho más detenimiento. En una próxima entrada volveremos sobre la investigación reproducible (y sus conexiones con la política y la economía, nada menos), sobre SWeave, y sobre la noción de Programación Literaria, que hizo posible todas estas ideas. Y (spoiler alert para profesores) sobre la forma de conectar todo esto con Moodle y usarlo en nuestras clases.

Gracias por la atención.

GeoGebra y la enseñanza de la Estadística

Con esta entrada inauguro una nueva sección del blog. Hasta ahora la mayoría de  las entradas tenían a mis alumnos como público objetivo principal (y por extensión a los alumnos de cursos de Introducción a la Estadística basados en R). Pero vamos a ir tratando, en esta y en futuras entradas algunos temas que van dirigidos a los profesores de ese tipo de ese cursos. Naturalmente, cualquiera puede leerlas, pero creo que es de rigor avisar de cuál es el lector que tengo en mente al escribir.

Por razones que explicaré más abajo, hasta ahora me he resistido todo lo que he podido a hablar de GeoGebra (enlace a la página oficial; es interesante además ver la página de la Wikipedia) en este blog. ¡Y sólo aquí! En realidad hace tiempo que hablo y no callo sobre el tema. Es, sin la menor duda, uno de los mejores programas para la enseñanza de las Matemáticas, desde la enseñanza primaria hasta la universidad. Creado por Markus Hohenwarter en 2001, ha ido ganando usuarios a un ritmo vertiginoso, sólo superado por el aún más vertiginoso ritmo al que el programa ha ido ganando en capacidades. Inicialmente, GeoGebra parecía ser uno más de los entornos de Geometría Dinámica (como Cabri, Cinderella o Sketchpad, por citar algunos). Pero la genialidad de su creador consistió en incorporar una doble representación de los objetos matemáticos, geométrica, pero también algebraica (de ahí el nombre). En la siguiente figura puede verse la interfaz habitual de GeoGebra (en la versión 4.2, la última oficial a fecha de hoy), con algunos objetos: una función, una recta, una circunferencia, puntos, etc. Y a la vez, en la vista algebraica, a la izquierda, aparece la descripción de esos objetos en una notación que, se acerca mucho (más con cada nueva versión de GeoGebra) a la notación algebraica habitual.

La vista gráfica de GeoGebra es una “pizarra con superpoderes”, puesto que los objetos tienen un carácter dinámico. Pero ante todo, el fundamento de su utilidad para la enseñanza es que mantiene la unidad de la representación habitual de los objetos matemáticos, a la que todos nos hemos acostumbrado en los libros de texto y en las clases. El usuario, con conocimientos de Matemáticas, que mira la ventana gráfica de GeoGebra, no necesita “traducción” de ningún tipo para reconocer la situación que tiene delante, porque el lenguaje es el habitual.

Conviene además recordar que GeoGebra es gratuito, de código abierto, y que cuenta con una auténtica legión de seguidores entusiastas.

¿Y GeoGebra tiene algo que ver con la Estadística? Hace unos años la respuesta hubiera sido: no mucho, salvo a costa de que el usuario hiciera bastante parte del trabajo por su cuenta. Pero ya decíamos que GeoGebra no deja de crecer. Y en las últimas versiones se han ido incorporando cada vez más características, que convierten al programa en una herramienta a tener muy en cuenta en la enseñanza de la Estadística. Vamos con algunas de ellas.

Los creadores de GeoGebra tuvieron, en algún momento de inspiración, la original idea de añadir, junto a las vistas geométrica y algebraica, una “vista de hoja de cálculo”, que se aprecia en la parte derecha de esta figura:

La hoja de cálculo es un primer paso hacia la Estadística, como bien sabemos. En el caso de GeoGebra, no obstante, lo que hace especial la hoja de cálculo es que el contenido de las celdas pueden ser objetos geométricos (puntos, rectas, curvas, etcétera), a los que se pueden aplicar operaciones en la forma habitual en una hoja de cálculo. Por ejemplo, si tenemos una columna de puntos, es posible marcar esa columna y trasladar todos los puntos simultáneamente mediante un cierto vector, obteniendo los puntos resultantes en otra columna. Es una forma muy interesante de trabajar, que da mucho juego en la enseñanza. Pero que nos desvía un poco de la temática del blog. La hoja de cálculo es una condición necesaria, pero no suficiente, para que GeoGebra juegue un papel en la enseñanza de la Estadística.

El paso definitivo (al menos para mi), sin embargo, se ha dado en las últimas versiones (esencialmente, a partir de la versión 4).  Ahora en uno de los menús de GeoGebra disponemos de la herramienta Cálculo de Probabilidades:

Al pulsar sobre esa herramienta se abre una nueva ventana, que ofrece una gran cantidad de posibilidades para el trabajo con las distribuciones de probabilidad (discretas y continuas) más habituales en los cursos de introducción a la Estadística:

Al abrir la ventana nos recibe la distribución Z (¿Cuál, si no?) Podemos usar los formularios y botones de esta ventana para estudiar problemas de probabilidad directa o inversa (cálculo de cuantiles o percentiles), tanto con colas como con intervalos. Además, desde luego, podemos modificar la media y desviación típica de la normal. También podemos, en lugar de la función de densidad, pulsar el pequeño botón que aparece al lado del nombre de la distribución, y cambiar la función de densidad por la de distribución, que se muestra en esta figura:

Esto mismo es posible con muchas otras distribuciones:

• continuas: t de Student, , F de Fischer, exponencial, Cauchy, Weibull, Gamma, LogNormal y Logística.
• Discretas: Binomial, Pascal, Poisson, Hipergeométrica.

Además, y de acuerdo con el espíritu dinámico de GeoGebra, podemos deslizar los puntos del eje x en la figura, y ver esos cambios reflejados automáticamente en los correspondientes valores de probabilidad. Dejo aquí enlazado un pequeño vídeo con una captura de ese tipo de manipulaciones dinámicas, que creo que ilustra los útil que puede llegar a ser GeoGebra en nuestras clases (se recomienda ver a pantalla completa).

Distribuciones de probabilidad con GeoGebra

Finalmente, en este breve recorrido de las posibilidades de GeoGebra, no quiero olvidarme de mencionar que (al margen de esta herramienta específica para las distribuciones más conocidas) GeoGebra ha incorporado una gran cantidad de comandos relacionados con la Probabilidad y la Estadística. En estas dos capturas de pantalla pueden verse las listas de comandos de GeoGebra para esos dos temas. De hecho la lista de comandos estadísticos es ya tan extensa que no cabe en esta captura…

                                       

En cualquier caso, el lector interesado podrá encontrar mucha más información aquí.

Gracias por la atención.