(Modificado el 20/01/2013 para corregir un error en la primera aparición de tapply)
Factores
En la octava sesión (se recomienda una relectura rápida de esa entrada antes de leer esta) hablamos de los datos de tipo character en R, que podían usarse, por ejemplo, para representar valores de variables cualitativas. Una situación frecuente en Estadística es esta: hemos medido una serie de valores de una variable cuantitativa X (es decir, los valores de X son números), pero esos valores aparecen agrupados de manera natural. Por ejemplo, cuando estamos midiendo la respuesta X (un número) de una serie de pacientes frente a varios tratamientos, es evidente que lo natural es agrupar los resultados según el tratamiento empleado. Una manera de hacer esto, en R, es usar un data.frame (ver la octava sesión) que contenga los valores de X, junto con los valores de una variable que indique el tipo de tratamiento empleado. Vamos a llamar
a los distintos tratamientos. La terminología estándar en Estadística es decir que el tratamiento T es un factor, y que sus valores son los niveles del factor. Podríamos entonces pensar en recoger los resultados en un fichero de datos como este, llamado experimento-01.csv. y trabajar así, usando variables de tipo character para los factores. Pero eso tendría un impacto negativo en el rendimiento de R. Y como los factores son omnipresentes en Estadística, R ha optado por incluir un tipo especial de vector para representar los factores y sus niveles. Y, de hecho, cuando leemos un fichero como el anterior usando read.table (de nuevo, remitimos al lector a la octava sesión). el comportamiento por defecto de R es convertir las variables cualitativas en factores.
Vamos a ver esto en funcionamiento. Guardaremos el contenido del fichero en un data.frame llamado experimento, con dos campos:
- experimento$Respuesta, de tipo numérico que almacena los valores de la variable X (la respuesta individual de cada uno de los pacientes).
- experimento$Tratamiento, de tipo factor que almacena los valores de la variable T (el tipo de tratamiento empleado).
Usaremos la función read.table para leer (y mostrar) el fichero, y luego la función class para ver el tipo de objeto que corresponde a cada uno de los campos del data.frame:
(experimento=read.table(file="experimento-01.csv",header =T, sep=" "))
class(experimento$Respuesta)
class(experimento$Tratamiento)
La ventana de resultados de Rcmdr, aparte de mostrar el contenido del fichero, indica que el campo experimento$Tratamiento es, en efecto, un factor.
¿Cómo se trabaja con factores en R? La contestación no puede ser completa, porque los factores son un ingrediente clave del lenguaje de R, e intervienen en muchísimas construcciones del sistema. Pero, en cualquier caso, podemos empezar por lo más sencillo.
¿Qué aspecto tiene un vector de tipo factor? En el caso del data.frame experimento que acabamos de crear, al mostrar el campo experimento$Tratamiento se obtiene esta salida:
> experimento$Tratamiento
[1] T1 T1 T4 T1 T2 T5 T5 T2 T5 T2 T3 T1 T5 T3 T3 T4 T1 T4 T1 T5 T4 T3 T4 T4 T1 T4 T1 T2 T3 T5 T5 T4
[33] T2 T4 T4 T5 T1 T3 T3 T1 T3 T2 T2
Levels: T1 T2 T3 T4 T5
Como se ve, R muestra el contenido del vector, junto con sus niveles. Si sólo queremos mostrar los niveles del factor, podemos usar la función levels, cuya salida es esta:
> levels(experimento$Tratamiento)
[1] "T1" "T2" "T3" "T4" "T5"
¿Qué significan esas comillas? Para entenderlo, es preciso conocer la diferencia que hay entre el vector experimento$Tratamiento y un vector de tipo character «con el mismo contenido«. Podemos apreciar la diferencia pidiendo a R que convierta el factor en character mediante la función as.character:
> as.character(experimento$Tratamiento)
[1] "T1" "T1" "T4" "T1" "T2" "T5" "T5" "T2" "T5" "T2" "T3" "T1" "T5" "T3" "T3" "T4" "T1" "T4" "T1"
[20] "T5" "T4" "T3" "T4" "T4" "T1" "T4" "T1" "T2" "T3" "T5" "T5" "T4" "T2" "T4" "T4" "T5" "T1" "T3"
[39] "T3" "T1" "T3" "T2" "T2"
Las comillas que aparecen en este caso indican precisamente que se trata de un vector de tipo character. Aunque los factores representan variables cualitativas, R los gestiona internamente mediante códigos numéricos. Al mostrarlos, a petición nuestra, el uso de las comillas permite distinguir entre character y factor.
Por cierto, cuando R carga un data.frame mediante read.table, los campos alfanuméricos (que contienen cadenas de texto, como el campo tratamientos de nuestro ejemplo) se convierten, por defecto en factores. Pero puede que, a veces, queramos preservar esos datos como variables de tipo character. Si es eso lo que queremos, basta con usar la opción stringsAsFactors=FALSE en la función read.table.
Los factores permiten modular el comportamiento de algunas funciones de R, de manera que la información que se obtiene tiene en cuenta esa organización en niveles de los valores que estamos analizando. Por ejemplo, en la quinta sesión vimos como usar la función summary para obtener un resumen descriptivo de un vector de datos (media y precentiles, básicamente). Ahora, que tenemos un data.frame con una clasificación por tratamientos, nos gustaría seguramente obtener esa misma información, pero para cada uno de los distintos tratamientos por separado. Lo primero que queremos hacer notar es que no sirve aplicar summary directamente al data.frame:
> summary(experimento)
Respuesta Tratamiento
Min. :2.600 T1:10
1st Qu.:4.540 T2: 7
Median :5.040 T3: 8
Mean :4.791 T4:10
3rd Qu.:5.250 T5: 8
Max. :6.060
Como se ve, se obtiene un resumen por separado para cada uno de los campos del data.frame: con Respuesta por un lado, y Tratamiento por otro, sin reconocer el vínculo entre ambas. Naturalmente, podemos ir separando cada uno de los grupos de tratamiento, y aplicarles la función summary a los vectores resultantes. Sería algo como esto (mostramos, por ejemplo el segundo grupo de tratamiento):ever
> (tratamiento1=experimento[experimento$Tratamiento=="T3",1])
[1] 5.41 4.87 5.68 5.34 5.71 5.24 5.06 4.52
> summary(tratamiento1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.520 5.012 5.290 5.229 5.478 5.710
Pero como se puede apreciar, trabajar así es engorroso. De hecho, la razón para incluir aquí esto es para poder mencionar el símbolo == que aparece ahí. En una próxima entrada, examinaremos con mucho más detalle ese símbolo, y todo lo que tiene que ver con los valores y operadores lógicos, como primer paso hacia la programación en R. Pero, para obtener lo que queremos, hay una manera mucho más natural de proceder, usando la función tapply. Veamos como funciona:
> attach(experimento)
> tapply(Respuesta,Tratamiento, summary)
$T1
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.700 4.955 5.080 5.079 5.228 5.370
$T2
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.600 3.110 3.180 3.214 3.335 3.830
$T3
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.520 5.012 5.290 5.229 5.478 5.710
$T4
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.400 4.605 4.975 5.058 5.400 6.060
$T5
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.560 4.935 5.015 5.039 5.182 5.390
El comando attach(experimento) le dice a R que vamos a usar el dataframe experimento, y nos permite usar las variables Respuesta y Tratamiento directamente por sus nombres, en lugar de tener que andar escribiendo experimento$Respuesta y experimento$Tratamiento todo el rato.
El resultado, como se ve, es una tabla (de ahí la t inicial de tapply) que contiene, ordenados por filas, los resultados de aplicar la función summary a los valores de Respuesta, agrupadas según los distintos niveles del factor Tratamiento.
Otro ejemplo de las ventajas del lenguaje de factores se obtiene al pensar en la función boxplot. Si aplicamos esa función directamente al data.frame, ejecutando
>
boxplot(experimento)
se obtiene un gráfico que no es, desde luego, el más apropiado, porque de nuevo se tratan respuestas y tratamientos por separado:
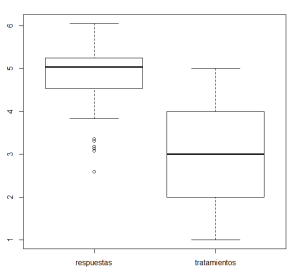
Para obtener lo que queremos basta con escribir:
>
boxplot(Respuesta~Tratamiento)
y el resultado es un gráfico mucho adecuado para comparar los resultados de los tratamientos:
La sintaxis Respuesta~Tratamiento que hemos usado en esta llamada es la que usa R para decir algo así como «la forma en que los valores de Respuesta dependen de los tratamientos«. En general, en R, el símbolo ~ se utiliza para indicar una dependencia o relación entre variables. En este caso, lo que estamos estudiando es si hay alguna relación entre la variable cualitativa (factor) Tratamiento, y la vaiable cuantitativa Respuesta. En particular, nos interesa saber si la respuesta media al tratamiento es distinta según el grupo de tratamiento que se considere. Se trata de un contraste de hipótesis, en la situación prototípica del método ANOVA unifactorial (¡porque sólo hay un factor, claro!) en el que, si llamamos
a las respuestas medias de la población tratada con cada uno de los grupos de tratamiento, la hipótesis nula del contraste,sería
Vamos a ver con más detalle algunas de las herramientas que R pone a nuestra disposición para llevar a cabo este tipo de contrastes ANOVA unifactoriales.
ANOVA unifactorial en R: hipótesis del modelo y tabla ANOVA
La teoría correspondiente se puede consultar en las notas de teoría, que están en esta entrada. Para empezar el trabajo de análisis con R, usaremos la función aov (de analysis of variance, claro) para calcular el modelo ANOVA y poder acceder a varias representaciones gráficas (por ejemplo, de los correspondientes residuos). La sintaxis sería algo como
aov(Respuesta~Tratamiento,datos)
siendo datos el dataframe que recibe como argumento, creado como hemos visto en el apartado anterior. La ventana de resultados de Rcmdr muestra una respuesta bastante concisa, que no incluye lo que solemos llamar la tabla ANOVA, ni el p-valor del contraste de igualdad de medias:
> (datos.aov=aov(Respuesta~Tratamiento,datos))
Call:
aov(formula = Respuesta ~ Tratamiento, data = datos)
Terms:
Tratamiento Residuals
Sum of Squares 20.968566 5.693996
Deg. of Freedom 4 38
Residual standard error: 0.3870943
Estimated effects may be unbalanced
Pero si se almacenan el resultado de la función aov en una variable, como hemos hecho nosotros con datos.aov, entonces se puede llamar a la función plot así:
plot(datos.aov)
para obtener un análisis gráfico de los residuos del modelo, que proporcionan información adicional, útil para saber si se cumplen los requisitos de aplicación del ANOVA. En particular, se obtiene una representación de los residuos frente a los valores predichos por el modelo (que son las medias), en la que debemos estar atentos a la aparición de posibles patrones en forma de cuña. En nuestro ejemplo, ese gráfico es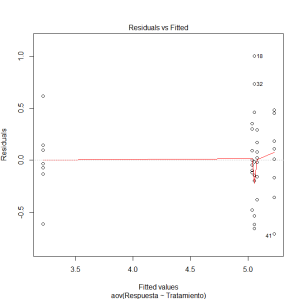 
y no se aprecia en el ningún patrón que indique un fallo evidente en las hipótesis del modelo (lo que se aprecia, de hecho, es que la media de uno de los grupos -niveles- del factor aparece claramente separada de las cuatro restantes; el resto del análisis confirmará esto).
También se obtiene el llamado QQ-plot (de quantile vs quantile), en el que se comparan las distribuciones de los residuos concretos de nuestros datos, con los que se obtendría si la muestra se ajustara exactamente a una distribución normal. Si las hipótesis del modelo se verifican, en este gráfico esperamos ver aparecer una nube de puntos situados muy aproximadamente a lo largo de una recta. En el ejemplo que nos ocupa, el gráfico QQ-plot es: 
y como puede verse, no es exactamente una recta, lo que sugiere que podemos tener algún problema con la hipótesis de normalidad en este ejemplo. ¿Qué hacemos, entonces? Bueno, por un lado, debemos tener presente que las muestras son pequeñas, así que, al igual que sucedía con los diagramas de cajas, el QQ-plot no es demasiado fiable como test de normalidad. En particular no sirve para garantizar que las poblaciones no son normales. Por otro lado, el contraste ANOVA es relativamente robusto frente a las desviaciones pequeñas de la normalidad, siempre y cuando las demás hipótesis del modelo se mantengan, y en particular cuando las varianzas de las poblaciones son homogéneas y todas las muestras son del mismo tamaño. En este ejemplo, esa segunda condición no se cumple, lo cual nos obliga a ser especialmente cautos. Vamos a empezar por dedicar nuestra atención a la homogeneidad de las varianzas.
Un primer paso puede ser un diagrama de varianzas frente a medias. En este ejemplo se obtiene: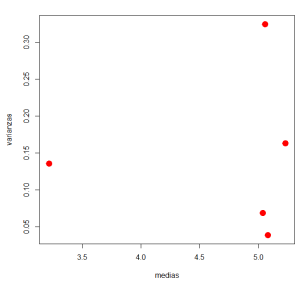 
Las varianzas de los grupos parecen ser bastante distintas, lo que podría preocuparnos, pero en este caso lo que más nos interesa es destacar que no hay relación aparente entre el tamaño de la medias y el tamaño de las varianzas. Esta información se une a la del diagrama de residuos frente a valores predichos. En este punto, y para obtener una representación alternativa de la dispersión, podemos volver a los boxplots paralelos por niveles del factor, que no contradicen a los otros gráficos. Como se ve, usamos toda la información disponible para ver si se detecta algún problema evidente, aunque en casos como este, con muestras tan pequeñas, es difícil ser concluyentes.
Antes de seguir adelante, una observación: puede pensarse en utilizar los diagramas de cajas para comprobar si la hipótesis de normalidad de las poblaciones del modelo se verifican. Pero debe tenerse en cuenta que en el caso de muestras pequeñas, no hay tal cosa como un diagrama de cajas representativo de una distribución normal. El siguiente fragmento de código R ilustra lo que decimos. Se calcula una muestra aleatoria (la media y la desviación típica también se eligen de forma aleatoria) de tamaño 10 de una distribución normal, y se dibuja su diagrama de cajas. Si se ejecuta este código, se verá que la forma de ese diagrama de cajas varía tanto de unas muestras a otras, que realmente no tiene sentido tratar de usar la forma de ese diagrama como comprobación de normalidad.
(media=runif(1,min=-10,max=10))
#(desvTip=sample(seq(from=0, to=abs(media)/2,length.out=100),1))
(desvTip=runif(1,min=0,max=abs(media)/2))
k=10
(muestra=rnorm(k,mean=media,sd=desvTip))
boxplot(muestra)
Y si quieres verlo de otra manera, aquí tienes un applet Java (hecho con GeoGebra, del que ya hablaremos en otra entrada) que ilustra el uso de los boxplots para comprobar la hipótesis de normalidad de una población a partir de sus muestras. Un poco más abajo volveremos sobre el tema del chequeo de la hipótesis de normalidad. El diagrama de boxplots paralelos tampoco parece ser de mucha utilidad para comprobar la homogeneidad de las varianzas. Es fácil usar R para comprobar que aproximadamente el 20% de las muestras de tamaño 10 de la normal estándar tienen desviaciones típicas que se alejan de 1 (la desviación típica de la población) en más de 0.3 unidades.
Volviendo a las hipótesis del modelo ANOVA, ¿cuál es la conclusión? La conclusión, como ya hemos dicho, es que es difícil ser concluyentes con muestras tan pequeñas. ¿Cómo vamos a proceder, entonces? Vamos a usar la tabla ANOVA para calcular el p-valor del contraste. Si ese p-valor es concluyente (en uno u otro sentido), confiaremos en la robustez del método frente a pequeñas desviaciones de las hipótesis. Naturalmente, si el p-valor se sitúa en el umbral de la región de rechazo, deberíamos ser mucho más cuidadosos, mirar con escepticismo las conclusiones y plantearnos la posibilidad de obtener muestras de mayor tamaño.
Para obtener la tabla ANOVA tenemos dos opciones. La primera es usar summary junto con la función aov que ya hemos visto. Recuérdese que hicimos
(datos.aov=aov(Respuesta~Tratamiento,datos))
La tabla ANOVA obtenida mediante summary(datos.aov) es:
> summary(datos.aov)
Df Sum Sq Mean Sq F value Pr(>F)
Tratamiento 4 20.969 5.242 34.98 2.91e-12 ***
Residuals 38 5.694 0.150
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
La otra opción es usar la sintaxis lm, de linear model, que en R se usa de forma genérica para representar la relación entre variables. De hecho, esta estructura lm juega un papel tan importante en R que, en breve, le dedicaremos una entrada. Para obtener la tabla ANOVA de esta manera hacemos:
anova(lm(Respuesta~Tratamiento,datos))
y el resultado es
> anova(lm(Respuesta~Tratamiento,datos))
Analysis of Variance Table
Response: Respuesta
Df Sum Sq Mean Sq F value Pr(>F)
Tratamiento 4 20.969 5.2421 34.984 2.906e-12 ***
Residuals 38 5.694 0.1498
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Como se ve, de una u otra manera, resultados son esencialmente iguales en este ejemplo. Y, en particular, el p-valor (2.906e-12) del contraste es extremadamente pequeño. Así que podemos rechazar la hipótesis nula, concluir que las medias son distintas, y a la vez estar relativamente seguros de que esta conclusión no depende de pequeñas desviaciones de las hipótesis del modelo.
En cualquier caso, el método ANOVA no agota, desde luego, el repertorio de recursos para realizar un contraste de igualdad de medios. Existen otros métodos, en especial métodos no paramétricos, que no dependen de las hipótesis de normalidad y homogeneidad de varianzas en la misma medida en que lo hace ANOVA. En R podemos usar uno de estos métodos para confirmar nuestras conclusiones, usando la función oneway.test. En concreto la forma de hacerlo es esta (se muestra la ventana de resultados):
> oneway.test(Respuesta~Tratamiento,datos)
One-way analysis of means (not assuming equal variances)
data: Respuesta and Tratamiento
F = 36.7064, num df = 4.000, denom df = 17.373, p-value = 2.946e-08
El p-valor (2.946e-08) de este método alternativo confirma la conclusión que habíamos obtenido utilizando ANOVA. ¿Por qué, entonces, no usamos siempre este método en lugar de ANOVA? La razón principal para hacerlo es que, cuando sus hipótesis se cumplen, el método ANOVA es, en general, más potente que este otro método.
Resultado significativo. ¿Y ahora qué?
Hemos rechazado la hipótesis nula, y por lo tanto, creemos que las medias de los distintos grupos son diferentes entre sí. El siguiente paso natural es, en muchos casos, tratar de comparar por parejas las medias. En nuestro caso eso significa comparar T1 con T2, T1 con T3, etcétera, hasta T4 con T5; un total de diez comparaciones, ya que
Pero no siempre queremos hacer esto; a veces sólo nos interesa comparar una media concreta con las restantes, en lugar de comparar todas las parejas posibles. En R se puede hacer esto usando summary combinado con lm de esta forma:
summary(lm(Respuesta~Tratamiento,datos))
y el resultado es:
> summary(lm(Respuesta~Tratamiento,datos))
Call:
lm(formula = Respuesta ~ Tratamiento, data = datos)
Residuals:
Min 1Q Median 3Q Max
-0.7087 -0.1590 -0.0180 0.1710 1.0020
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.07900 0.12241 41.492 < 2e-16 ***
Tratamiento[T.T2] -1.86471 0.19076 -9.775 6.4e-12 ***
Tratamiento[T.T3] 0.14975 0.18361 0.816 0.420
Tratamiento[T.T4] -0.02100 0.17311 -0.121 0.904
Tratamiento[T.T5] -0.04025 0.18361 -0.219 0.828
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
¿Cómo se interpreta esto? La parte más importante para nosotros es la tabla que aparece bajo el epígrafe Coefficients. En esa tabla aparecen los contrastes de igualdad de medias de T1 (el primer nivel del factor; en el orden en que nosotros los hemos ordenado, claro) con el resto de los niveles. El valor que aparece al lado de (Intercept) es simplemente la media del primer grupo (el de T1), mientras que en las restantes filas de la columna Estimate aparecen las diferencias entre las medias de T1 y las de los restantes niveles. Por ejemplo, la diferencia entre las medias de los tratamientos T1 y T4 es -0.02100. Y el p-valor para el contraste de diferencia de medias entre T1 y T4 está en la última columna, y vale 0.904. Los resultados de esta tabla indican que la media de T1 es significativamente distinta de T2 (tal vez sea buena idea volver a mirar los boxplots paralelos), mientras que no hay diferencias significativas entre la media de T1 y la de los tratamientos T3, T4 y T5.
Naturalmente, esta forma de trabajar privilegia a T1 frente a los demás tratamientos, y no responde a preguntas como ¿hay diferencia significativa entre T3 y T5? Para obtener la información de los diez contrastes por parejas posibles utilizamos la función pairwise.t.test de R, de esta manera (se muestra la ventana de resultados):
> pairwise.t.test(datos$Respuesta,datos$Tratamiento, p.adj="bonferroni")
Pairwise comparisons using t tests with pooled SD
data: datos$Respuesta and datos$Tratamiento
T1 T2 T3 T4
T2 6.4e-11 - - -
T3 1 2.9e-11 - -
T4 1 8.7e-11 1 -
T5 1 4.3e-10 1 1
P value adjustment method: bonferroni
En la tabla que aparece hay, en efecto, diez p-valores (se evitan las duplicidades mostrando sólo los valores de la parte de la tabla bajo la diagonal). Con esos p-valores podemos establecer qué parejas de medias son relamente distintas. En este ejemplo la conclusión (que ya avanzaban los boxplots) es que la media de T2 es significativamente distinta de todas las demás, pero que no hay diferencias significativas entre T1, T3, T4 y T5 (los p-valores correspondientes son – aproximadamente – 1). Sabemos (ver las notas de teoría), que es preciso ser cuidadosos a la hora de calcular esos p-valores, porque la simple repetición de diez contrastes aumenta mucho la probabilidad de cometer errores de tipo I. Así que R aplica alguno de los métodos habituales (hay varias estrategias, de nuevo remitimos a las notas de teoría y la bibliografía que allí aparece) para ajustar esos p-valores de manera que el error de tipo I se mantenga bajo control. Aquí hemos optado por pedirle a R que utilice la más clásica y conocida de esas estrategias, la de Bonferroni.
Estos contrastes por parejas, incluso cuando se usan correcciones como la de Bonferroni, dependen de la hipótesis de normalidad de las poblaciones correspondientes a los factores. Para reducir la dependencia de nuestras conclusiones de esa hipótesis, podemos utilizar algún método no paramétrico, de forma similar a lo que hicimos con la tabla ANOVA. En este caso, el método más conocido para realizar el contraste es el de Tukey. Sin entrar en detalles, la forma de aplicarlo en R es esta (se muestra la ventana de resultados):
> summary(glht(datos.aov, linfct = mcp(Tratamiento = "Tukey")))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = Respuesta ~ Tratamiento, data = datos)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
T2 - T1 == 0 -1.86471 0.19076 -9.775 <1e-05 ***
T3 - T1 == 0 0.14975 0.18361 0.816 0.924
T4 - T1 == 0 -0.02100 0.17311 -0.121 1.000
T5 - T1 == 0 -0.04025 0.18361 -0.219 0.999
T3 - T2 == 0 2.01446 0.20034 10.055 <1e-05 ***
T4 - T2 == 0 1.84371 0.19076 9.665 <1e-05 ***
T5 - T2 == 0 1.82446 0.20034 9.107 <1e-05 ***
T4 - T3 == 0 -0.17075 0.18361 -0.930 0.883
T5 - T3 == 0 -0.19000 0.19355 -0.982 0.861
T5 - T4 == 0 -0.01925 0.18361 -0.105 1.000
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)
Que es, en esencia, de nuevo una tabla con los diez p-valores, que viene a confirmar lo que habíamos obtenido anteriormente (observar los astericos a la derecha de la última columna, y su significado bajo la tabla; hay cuatro contrastes significativos, todos con T2 y uno de los otros grupos).
Representaciones gráficas. Bargraphs y otras opciones.
Después de un análisis como el que hemos hecho, los gráficos son una de las formas más comunes de presentar los resultados. Una de las representaciones gráficas más populares, pese a sus inconvenientes son los gráficos de columnas adaptados para incluir líneas de error, como este para el ejemplo que nos ocupa: 
Pero hay que tener en cuenta que los gráficos de columnas se concibieron para representar frecuencias, no medias. Y en estos gráficos de columnas adaptados aparece un nivel de referencia (la base de las columnas, que en este caso R ha situado de forma automática en 3), nivel que a menudo no tiene ningún significado real en el contexto del problema que estamos estudiando. Como puede verse, las barras, cuya altura se corresponde con la media de cada uno de los grupos, se acompañan de una línea o barra de error adicional. Un problema añadido de estos diagramas es que, en muchos casos, no está claro si esas líneas de error representan intervalos de confianza (y cuál es en ese caso el nivel de confianza), o errores estándar, o alguna otra medida de dispersión. Hay que subrayar que debe dejarse siempre claro, en el texto que acompañe a la figura, cuál es la medida de dispersión que se ha utilizado. Una alternativa es eliminar las columnas, y representar siempre en paralelo intervalos de confianza para la media, como en este gráficoque corresponde a nuestro ejemplo (la idea procede del capítulo 7 de Introductory Statistics with R, 2nd Ed, de P.Daalgard):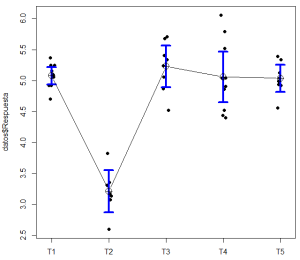
Se muestra la nube de puntos correspondiente a cada muestra, y barras que corresponden con intervalos de confianza para cada una de esas medias. En este caso la única información necesaria para la correcta interpretación del gráfico es el nivel de confianza de esos intervalos.
Formato del fichero de datos y conclusión
Durante todo el trabajo anterior hemos usado un fichero de datos, llamado experimento-01.csv,.en el que los datos de la respuesta por grupos se presentan en dos columnas. La primera columna contiene el valor numérico de la respuesta, y la segunda el nivel (grupo) del factor Tratamiento. En otras ocasiones esa misma información se puede presentar de otra manera, con cada uno de los grupos/niveles ocupando su propia columna, como en este fichero experimento-01a.csv, que contiene los mismos datos del ejemplo que hemos usado. El capítulo correspondiente de las notas de teoría contiene un fichero de código (y esa será la versión que en el futuro trataré de mantener actualizada) para el análisis ANOVA unifactorial, que permite realizar todos los pasos del análisis que hemos descrito en esta entrada. Este fichero trata de reconocer automáticamente el formato de entrada del fichero de datos (en las dos situaciones más comunes, las que hemos descrito), para realizar el análisis correcto. Es conveniente comprobar, en cualquier caso, que los datos se han reconocido correctamente y que no aparece ningún mensaje de error en la lectura. Ese reconocimiento automático utiliza estructuras de programación de R. La existencia de esas estructuras de programación es una de las razones que hacen de R una herramienta tan versatil y potente, así que volveremos sobre ellas en próximas entradas.
Gracias por la atención.
. Y si usamos esta segunda ordenación de las muestras, puesto que ahora el valor del estadístico es mayor que uno, tenemos que usar la cola derecha de la distribución, como ilustra esta figura (no es la misma F de antes; los grados de libertad también han intercambiado sus posiciones):
y la cuasivarianza 
, y el tamaño n de la muestra), y pedirle a R que haga el contraste usando esos valores 
, y mediante las opciones alternative = c(«greater») y conf.level = 0.95 hemos seleccionado un contraste de cola derecha (greater, o mayor que) y el nivel de significación deseado (conf.level, R usa la misma terminología que para los intervalos de confianza) .
de la variable X cuya densidad es f(x)? Recordemos que, si la densidad de X en (a,b), es una función f(x), entonces la media de X es:
como valor de la media.
(y desviación típica) de X. Ahora, recordando que la fórmula para la varianza es
. La desviación típica es simplemente la raíz cuadrada de este número (calculada, por ejemplo, con la función sqrt de R).
.
(es decir, $\latex \mu=3, \sigma=2$ y X=4) usaríamos un código como este:
hasta 
, usaremos el comando curve de esta manera
y queremos calcular la probabilidad
,
.
(n es el número de ensayos y p la probabilidad de éxito en cada uno de esos ensayos) toma valores k de 0 a n, y se cumple que
la probabilidad de fallo.
).
? Para responder a este tipo de preguntas en R disponemos de la función qbinom. Concretamente, obtenemos la respuesta ejecutando:
(la media de X) y 
(la desviación típica de X), y vamos a aprender a utilizar R para calcularlos. Para fijar ideas vamos a pensar en un ejemplo concreto. Supongamos que la densidad de probabilidad de la variable X es esta:
, debemos hacer:
para cada $k$.
PostData 